Kilas Berlajar Singkat

Principal Component Analysis (PCA) sebagai Metode Jitu Untuk Mengatasi Masalah Multikolinearitas

Masalah Multikolinearitas dalam Regresi Berganda

Istilah Multikolinearitas pertama kali ditemukan oleh Ragnar Frisch yang berarti adanya hubungan liniear yang sempurna atau pasti diantara beberapa atau semua variabel bebas dari model regresi berganda.

Menurut Gujarati (1978) gejala Multikolinearitas ini dapat dideteksi dengan beberapa cara antara lain :

1. Menghitung koefisien korelasi sederhana (simple correlation) antara sesama variabel bebas, jika terdapat koefisien korelasi sederhana yang mencapai atau melebihi 0.8 maka hal tersebut menunjukkan terjadinya masalah multikolinearitas dalam regresi.
2. Menghitung nilai Toleransi atau VIF (Variance Inflation Factor), jika nilai Toleransi kurang dari 0.1 atau nilai VIF melebihi 10 maka hal tersebut menunjukkan bahwa multikolinearitas adalah masalah yang pasti terjadi antar variabel bebas.
3. Lakukan regresi antar variabel bebas dan menghitung masing-masing R2 , kemudian melakukan uji – F dan bandingkan dengan Ftabel (a;k-2,n-k+1). Jika nilai Fhit melebihi nilai Ftabel berarti dapat dinyatakan bahwa Xi kolinier dengan X yang lain.

Akibat dari masalah Multikolinearitas

Montgomery dan Hines (1990) menjelaskan bahwa dampak multikolinearitas dapat mengakibatkan koefisien regresi yang dihasilkan oleh analisis regresi berganda menjadi sangat lemah atau tidak dapat memberikan hasil analisis yang mewakili sifat atau pengaruh dari variabel bebas yang bersangkutan. Dalam banyak hal masalah Multikolinearitas dapat menyebabkan uji T menjadi tidak signifikan padahal jika masing-masing variabel bebas diregresikan secara terpisah dengan variabel tak bebas (simple regression) uji T menunjukkan hasil yang signifikan. Hal tersebutlah yang sering kali membuat pusing para peneliti karena hasil analisis yang dilakukan pada regresi berganda dan regresi sederhana tidaklah sejalan atau bahkan sangat bertentangan.

Contoh Ilustratif :

X1 = KADAR GULA
X2 = KADAR MADU
X3 = KADAR SUSU
Y = RASA MINUMAN SEHAT


Pada ilustrasi di atas tampak bahwa antara gula (x1) dengan madu (x2) akan membawa dampak yang sama (atau saling berhubungan) terhadap rasa manis pada minuman, sehingga akan sangat sulit untuk mengukur pengaruh rasa manis gula dan pengaruh rasa manis madu secara terpisah terhadap rasa minuman karena pengaruh rasa manisnya gula telah tercampur dengan rasa manisnya madu.

Prosedur Penanggulangan Masalah Multikolinearitas
Ada beberapa prosedur yang dapat digunakan untuk mengatasi masalah multikolinearitas, seperti : penggunaan informasi apriori dari hubungan beberapa variabel yang berkolinear, menghubungkan data cross-sectional dan data time series, mengeluarkan suatu variabel atau beberapa variabel bebas yang terlibat hubungan kolinear, melakukan transformasi variabel dengan prosedur first difference dan penambahan data baru. Akan tetapi pada prakteknya prosedur penanggulangan yang telah disebutkan di atas sangat tergantung sekali pada kondisi penelitian, misalnya : prosedur penggunaan informasi apriori sangat tergantung dari ada atau tidaknya dasar teori (literatur) yang sangat kuat untuk mendukung hubungan matematis antara variabel bebas yang saling berkolinear, prosedur mengeluarkan variabel bebas yang berkolinear seringkali membuat banyak peneliti keberatan karena prosedur ini akan mengurangi obyek penelitian yang diangkat, sedangkan prosedur lainya seperti menghubungkan data cross sectional dan time series, prosedur first difference dan penambahan data baru seringkali hanya memberikan efek penanggulangan yang kecil pada masalah multikolinearitas.

Principal Component Analysis (PCA) Mengatasi Masalah Multikolinearitas
Prosedur PCA pada dasarnya adalah bertujuan untuk menyederhanakan variabel yang diamati dengan cara menyusutkan (mereduksi) dimensinya. Hal ini dilakukan dengan cara menghilangkan korelasi diantara variabel bebas melalui transformasi variabel bebas asal ke variabel baru yang tidak berkorelasi sama sekali atau yang biasa disebut dengan principal component.

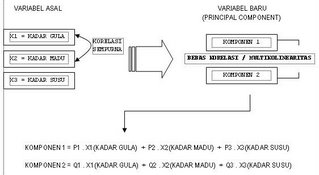KOMPONEN 1 = P1 . X1(KADAR GULA) + P2 . X2(KADAR MADU) + P3 . X3(KADAR SUSU)
KOMPONEN 2 = Q1 . X1(KADAR GULA) + Q2 . X2(KADAR MADU) + Q3 . X3(KADAR SUSU)


Setelah beberapa komponen hasil PCA yang bebas multikolinearitas diperoleh maka komponen-komponen tersebut diregresikan atau dianalisa pengaruhnya terhadap variabel tak bebas (Y) dengan menggunakan analisis regresi berganda. Analisis regresi akan menghasilkan model regresi sebagai berikut :



Y(RASA MINUMAN SEHAT) = B1 . KOMPONEN 1 + B2 . KOMPONEN 2



Dengan menggunakan prosedur subtitusi variabel dan perhitungan nilai standart error koefisien regresi, maka pengaruh x1, x2 dan x3 akan dapat dipelajari dan disimpulkan pengaruhnya terhadap rasa minuman.


Keuntungan penggunaan Principal Component Analysis (PCA) dibandingkan metode lain :

1. Dapat menghilangkan korelasi secara bersih (korelasi = 0) sehingga masalah multikolinearitas dapat benar-benar teratasi secara bersih.
2. Dapat digunakan untuk segala kondisi data / penelitian
3. Dapat dipergunakan tanpa mengurangi jumlah variabel asal
4. Walaupun metode Regresi dengan PCA ini memiliki tingkat kesulitan yang tinggi akan tetapi kesimpulan yang diberikan lebih akurat dibandingkan dengan pengunaan metode lain